The Math Intercept 10
Window Game, Galileo's Sequence, Strands, Global CO2 Emissions, Emma Kunz and more...
Hello everyone, it is time for another Math Intercept! Welcome.
Recently, we have been trying to invent some new math games at home with my two young mathematicians. The first game is called the Window. We are still developing it, but here is how it looks:
There are two players, and each player uses either X or O like in Tic-Tac-Toe.
One of them starts from anywhere on a 5x5 grid. (In the below examples X is player 1)
The aim is to cover a window:
In a single round it is possible to claim more than one window, but a player cannot claim two windows with one attempt.
When the grid is completed, the player with more windows wins.
Here is an example:
There are certain parts to improve yet, work in progress!
The second game we came up with was “the L Game”. However, after some turns I thought that somebody might actually invented a game like this before, and there I was right, 🫤. It is called Joust. That game is played with two knights on the chess board. In our version the players start randomly somewhere on a 5x5 board and continue marking the boxes with O and X in turns following the L movement as the knight moves in a chess game.
We played few times yet, so the young boys have not identified any strategies so far.
The New York Times has some wonderful games on their website and recently they have been testing a new game called Strands. The first time I saw and solved this game there was a beautiful surprise awaiting:
Math Eyes: Curves

Math In Action
John Eglin from the University of Montana writes on the role of mathematics in the development of gambling industry in the 18th century. After Bernoulli brothers proved their Golden Theorem (The Law of Large Numbers or Long averages), gambling houses slowly noticed that the house edge, where the casino has a small advantage, was crucial to the profitability of their businesses. Even a small edge could result in significant profits over time. This changed the whole game and we have the big industry today.
This research paper describes a new mathematical method to quantify how quickly proteins break down in cells. This is important because understanding protein degradation rates can help us understand aging and other biological processes. The mathematical technique used is called maximum entropy. This method is used to find the most likely answer to a problem when there are many possible solutions. In this case, the problem is to determine the degradation rates of all the proteins in a cell, based on limited experimental data. The researchers found that proteins can be classified into three categories based on their degradation rates: minutes, hours, or days. They also studied how protein degradation rates change in response to starvation. This could have implications for understanding muscle wasting in cancer patients. In short, the math involved finding the most probable protein degradation rates based on limited data (like a blurry picture).
Proofs Without Words
Galileo’s Property of Sequence of Odd Integers (1615)

It is amazing that this is going back to Galileo! The image created by Nelsen is a true example of “proof without words”.
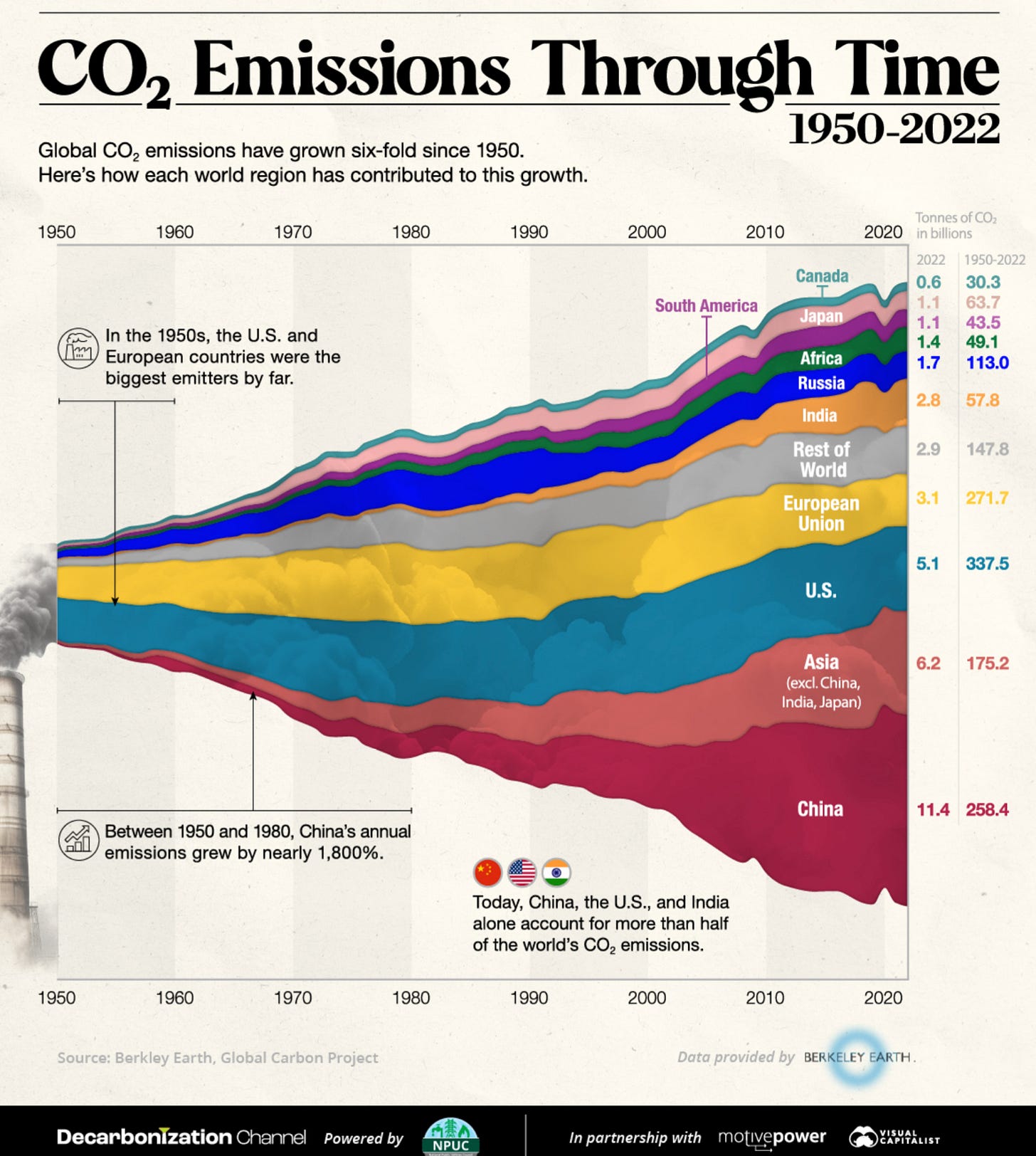
What is going on in this graph?
Global CO2 emissions are the release of carbon dioxide into the atmosphere as a result of human activities. Carbon dioxide is the primary greenhouse gas that contributes to global warming.
The main sources of global CO2 emissions are:
Fossil fuel burning (coal, oil, and natural gas) for electricity, heat, and transportation
Industrial processes, such as cement production and steel manufacturing
Land use changes, such as deforestation
Global CO2 emissions have been increasing steadily for decades, and they are now at their highest level in history. This is causing the Earth's climate to change at an unprecedented rate.
The effects of global warming are already being felt around the world, and they are expected to become more severe in the future. These effects include rising sea levels, more extreme weather events, such as heat waves, droughts, floods, and wildfires, changes in precipitation patterns, ocean acidification and loss of biodiversity.
Global warming is a serious threat to the planet and its inhabitants. It is important to take action to reduce CO2 emissions in order to mitigate the effects of climate change.
In the mid-20th century, the USA and future European Union countries were the world's top polluters, creating over 70% of yearly emissions. This dominance quickly shifted as other countries joined the game. China's economic boom in the 1970s, fueled by a new economic policy, led to a dramatic rise in their CO2 emissions. By 2000, China's emissions had grown over 45 times compared to 1950, reaching 3.6 billion tonnes annually. This trend wasn't unique to China. India, Japan, and the rest of Asia also saw their emissions skyrocket by over 10 times between 1950 and 2000.
Sources:
https://decarbonization.visualcapitalist.com/global-co2-emissions-through-time-1950-2022/
https://www.motive-power.com/national-public-utilities-council/?utm_source=decarb-channel&utm_medium=sponsored-content&utm_campaign=Decarbonization
Curious Puzzles
This time I am attempting creating a Strand puzzle. Let’s see if you can find the words.
Answers to Last Issue Puzzles
Ask a friend to pick a number from 1 through 1000. After asking them 10 questions that can be answered with yes or no, you tell them the number. What kind of questions should you ask your friend so that you find their number? (Kordemsky, The Moscow Puzzles)
The key to the solution is that 2 to the tenth power is 1,024 (that is, over 1,000). With each question you knock out half the remaining numbers, and after ten questions only the "thought" number is left. Say the number is 860. The ten questions are:
1. "Is your number greater than 500?" "Yes." Add 250.
2. "Greater than 750?" "Yes." Add 125.
3. "Greater than 875?" "No." Subtract (not 62½ but the nearest even number) 62.
4. "Greater than 813?" "Yes." Add 31.
"Greater than 844?» "Yes." Add (not 15½ but) 16.
6. "Greater than 860?" "No." Subtract 8.
7. "Greater than 852?" "Yes." Add 4.
"Greater than 856?" "Yes." Add 2.
9. "Greater than 858?" "Yes." Add 1.
10. "Greater than 859?" "Yes."
The number is 860.
Can you find the values of the letter making the following equation correct?
J=5, O=7, K=1, I=4, N=2 and G=8
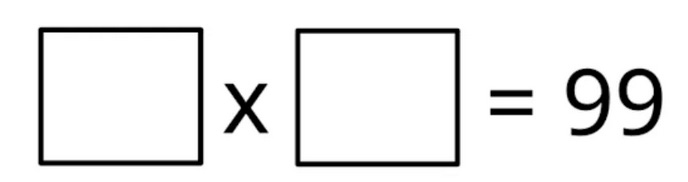
Find two rational numbers to fill the boxes. They must be both less than 10.
There can be many answers: For example:
9900/1000 and 1000/101
189/19 and 209/21
Math In Art: Emma Kunz

Emma Kunz (1892-1963) was a unique personality as her career cannot be fit into one category. She was known as a healer, but her research into spiritual world took her into art in which she used pendulums to express her understanding of health and universe using art.
Goodreads: Mathemalchemy
Mathemalchemy is a community of “twenty-four mathematical artists and artistic mathematicians” that aim to celebrate the beauty and creativity of mathematics through a variety of art forms. One of their products is a comic book. Created by Jay and Max Hosler, the book tells the story of a child and her mother’s mathematical adventures.
Mathemania
I hope you enjoyed the Math Intercept. See you in the next adventure.