The Math Intercept 3

Stemco Math Competition, Soap Bubbles, World ad 1000 people and more

Nov 24, 2023

Hey everyone,

Here comes the third of the Math Intercept! Some of my students are participating in a Singapore-based math and science competition named Stemco these weeks. As mathematics Olympiads require years of training and specialization, they usually appeal few students. This competition, however, has a different style, they are more based on conceptual understanding and seem to have a lot of resemblance to the International Baccalaureate (IB) framework. Moreover, students are allowed to use AI while answering questions!

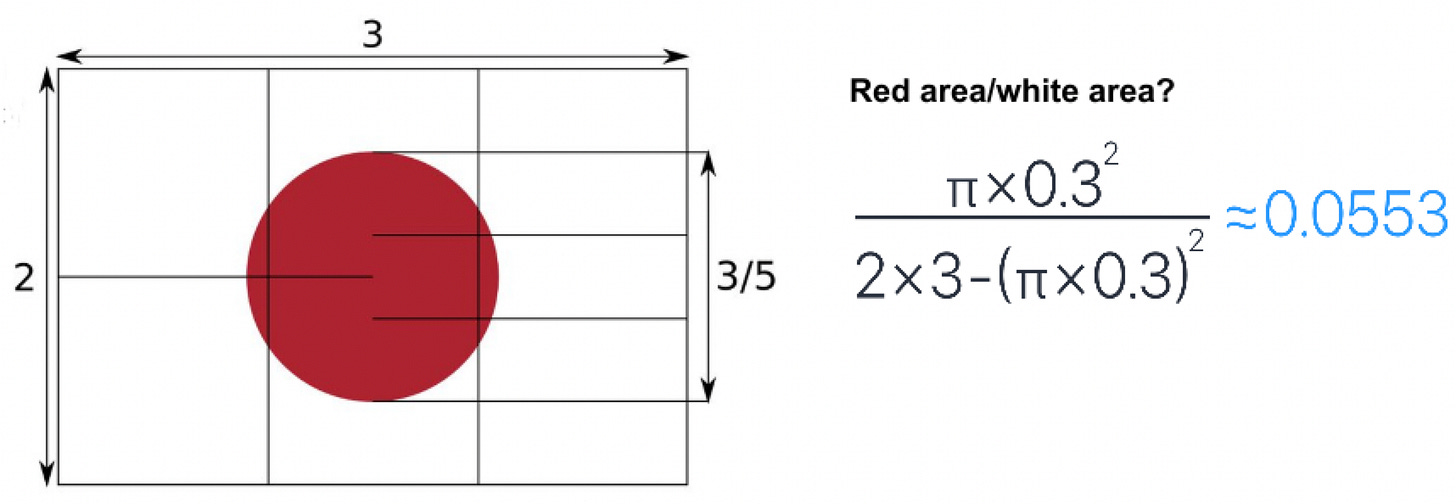
Math Eyes: The Math of Soap Bubbles

Adrienne Bresnahan/Moment via Getty Images

Soap bubbles are a great example of minimal surfaces, which have the least possible area for a given volume. A true minimal surface is a soap film with equal pressure on both sides, while a soap bubble is a closed soap film with different pressures on each side. Soap bubbles have been used to solve practical problems, such as designing structures with the least possible surface area.

Soap bubbles form hexagonal patterns when they are closely packed together. This is because hexagons are the most efficient way to pack circles together, meaning they can fit together without gaps or overlaps. This allows the soap bubbles to minimize their surface area, which is important because surface tension pulls them into shapes with the least possible surface area.

[Check here, here, and here for the sources and further reading.]

Curious Puzzles: Look and Say Puzzles

We have look-and-say puzzles in this edition. It is a popular one, but may look weird at first if you did not encounter with them before.

1, 11, 21, 1211, 111221, 312211,?
2, 12, 1112, 3112, 132112,?
When you start the sequence with 12 in Q2, you will see that the sequence keeps going forever. However, there is an exception to this. What is the starting number for a limited sequence?
?, ?, ?, 31131211, ...

Answers for the Puzzles from the previous issue

A ticket and an ice cream cost $20. I paid $17 more for the ticket than for the ice cream. What are their prices?
$1.5 vs $17.5
Only one of these statements is true. Which one?

The answer is E. If F is true, then E is also true. E must be the only true one.

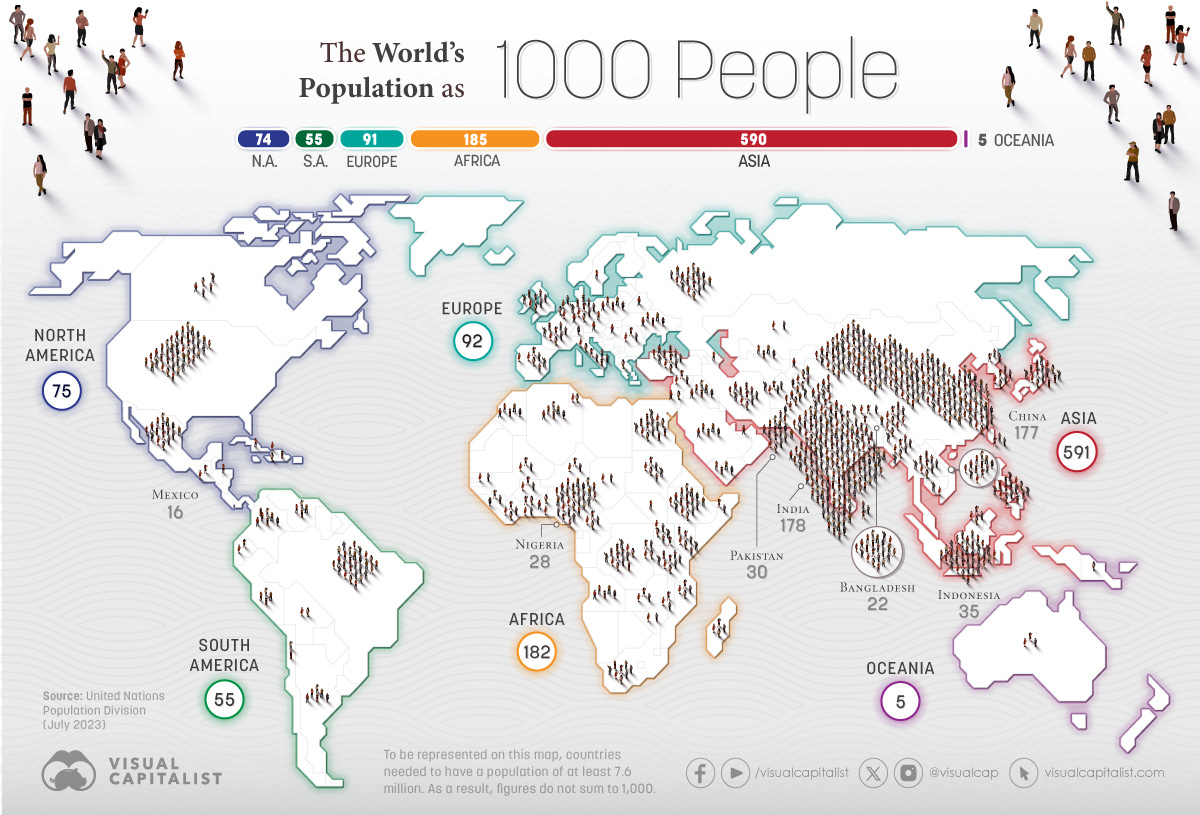
What is going on in this graph?

Map of all the people in the world if there were only 1,000 people

If there were 1000 people in the world, 182 of them would be in Africa, 178 of them would be in India and 177 of them would be in China. This is about 54% of the whole world. Asia alone makes the 59% of the world. We can make these kinds of calculations using the population amounts of continents and countries of course. The above graphic visually shows us where each population is located. We can see how crowded India and China are. It is interesting to see how empty Australia is. The drawback of this visual? It seems New Zealand and Iceland are remote islands with no humans on them! 🫢

You can read more on Visual Capitalist’s website.

Share The Math Intercept

Math In Action

In environmental science, a tipping point is a critical threshold that, when crossed, leads to large, accelerating, and often irreversible changes in an environmental system. These changes can have far-reaching and potentially disastrous consequences for ecosystems, human societies, and the planet as a whole. The Atlantic Meridional Overturning Circulation (AMOC) is one of these tipping points. AMOC regulates the climate in Europe and North America by the warm water it brings. Its collapse will cause a huge disruption to the North Atlantic climate systems. This new study introduces powerful mathematical tools that are crucial for comprehending and forecasting climate change, particularly for identifying and averting climate tipping points brought on by human actions.
A 17 year-old student used quadratic approximation to predict his blood cell count. He watched and learned calculus through MITx, and is still working on understanding his cancer treatment. He spoke to MIT News on the matter and commented the following: “I want to research it, find ways to help people get rid of their cancer, and better patients’ treatment.”.
A Guardian article written by Emma Beddington points interesting details on peak points we reach after the age of 40. The author claims that some cognitive abilities, such as arithmetic problem-solving, peaked later in life, around age 50.