The Math Intercept 6
The Spiral of Theodorus, Hyperboloid Structures, Cliodynamics and more
Greetings math lovers,
It has been a while. After a long break here is the first Math Intercept of 2024.
❁❁❁
I have been teaching Pythagorean Theorem in my Grade 8 classes. There, we discussed how it is possible to measure the immeasurable in mathematics. Square roots are mostly irrational numbers, for example, √2 gives a never-ending decimal. An isosceles right-angled triangle with perpendicular sides of 1 unit will have √2 as its hypotenuse. So even though we cannot know the number itself exactly, we can still construct the length and the triangle. In one of the classes we worked on an activity called “The Spiral of Theodorus”. The spiral starts with the triangle above and extends by a perpendicular length of 1 unit. Since the other perpendicular length is the hypotenuse of the previous step, the shape turns into a spiral. Below are some student constructions:
❁❁❁
Recently, a prime number that consists of 1800 digits went viral after Elon Musk highlighted the X logo on it. A brilliant advertisement. He calls it Prime Real Estate. Among the 1800 digits made of 1s and 8s, one 7 could sneak inside.
❁❁❁
Math Eyes: Hyperboloid Structures
A hyperboloid is a quadratic surface and can be achieved by rotating hyperbolas around central axes. Hyperboloid structures are used in architecture in various forms.
❁❁❁
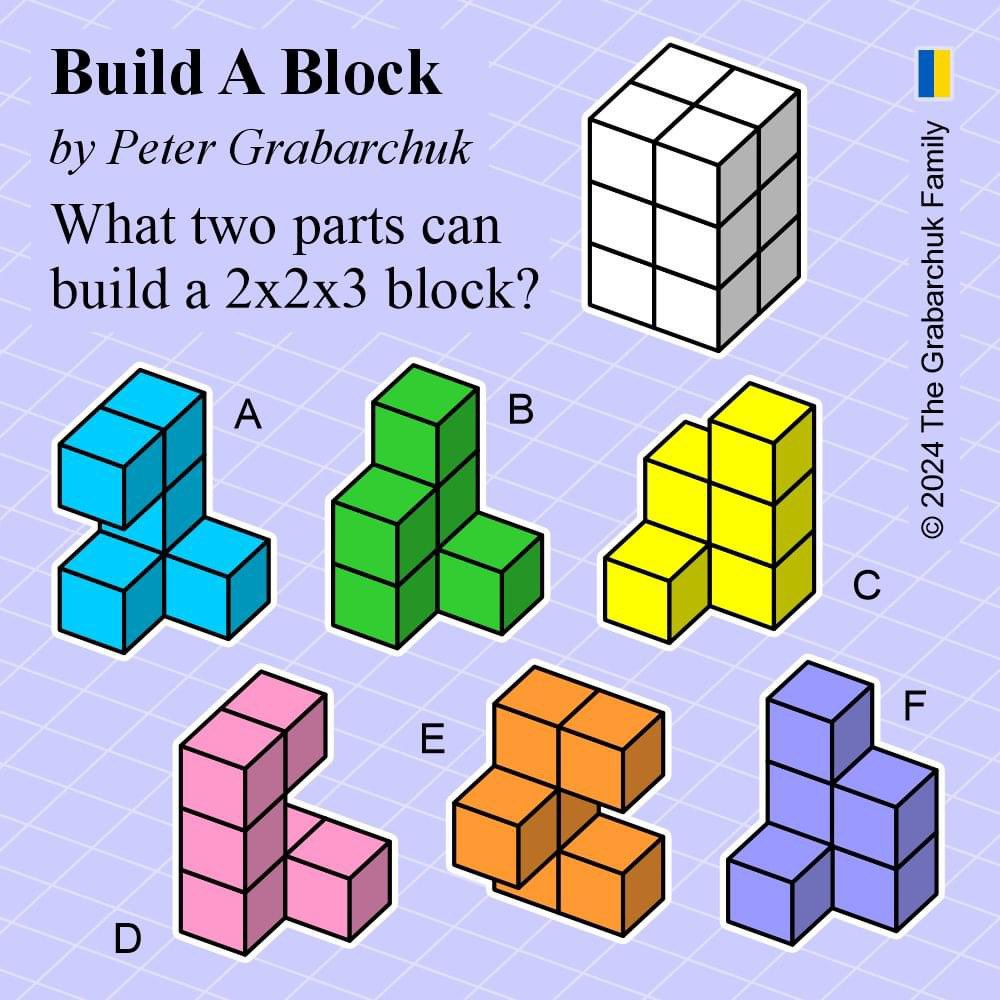
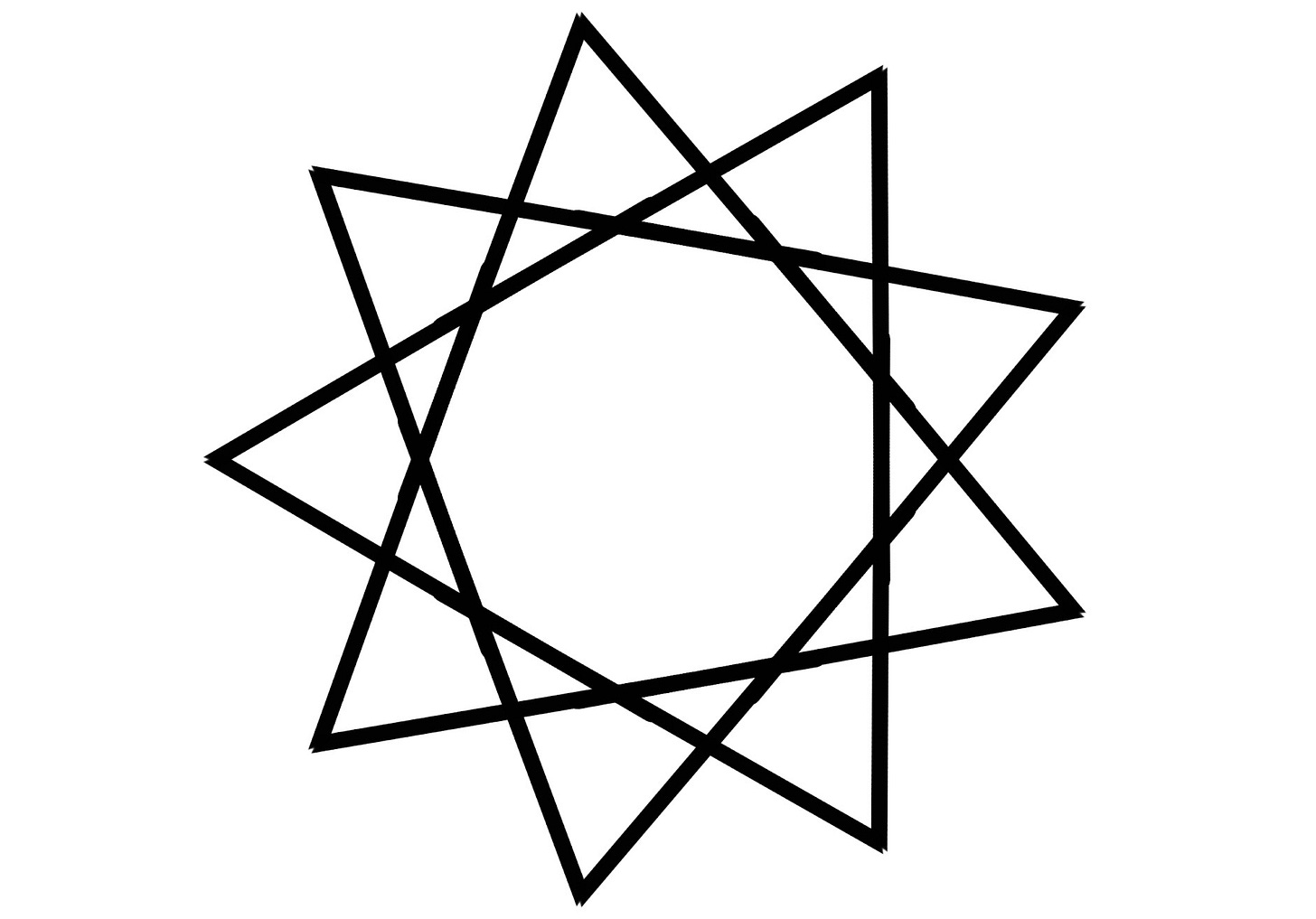
Curious Puzzles:
I like the style of Grabarchuk puzzles. The first puzzle comes from them.
How many triangles can you count? (All lengths are straight lines)
❁❁❁
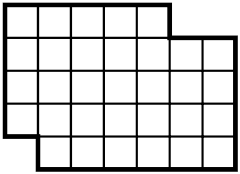
Answers for the Puzzles from the previous issue
You are given a 5-by-7 rectangle with two corners cut out: A 1-by-1 tile is cut from the bottom left corner, and a 1-by-2 tile is cut out of the top right corner, as in the picture. The task is to cut the resulting shape into two congruent polyominoes. [credits for the puzzle: Tanya Khovanova]
(95/247)+(86/13)
❁❁❁
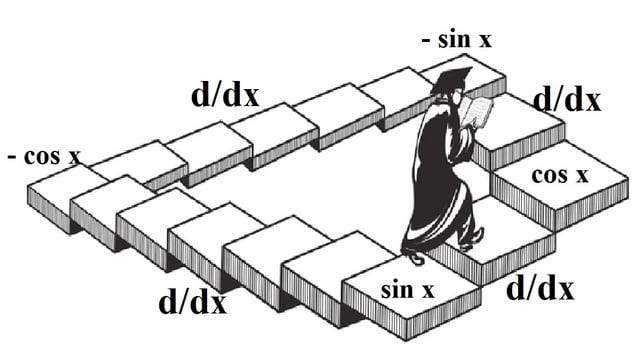
Proofs Without Words
❁❁❁
Math in Action
Cliodynamics
Cliodynamics is the field of study that combines cultural evolution, economic history, sociology, and mathematical modeling to explore the long-term patterns and dynamics of human societies. In this field, by using mathematical models, researchers can test hypotheses and make predictions about how societies might behave under different conditions.
For example in a recent research published in PNAS Nexus, researchers used data from 370 societies across 10,000 years to estimate cultural evolution rates. They found similar patterns in 23 geographic regions, suggesting societies take around 2,500 years to reach high complexity, achieved through multiple cultural phases. This implies shared pathways in human social evolution across different cultures.
❁❁❁
This article suggests that the emerging patterns of cicadas and stock market crashes could be modeled by similar mathematical models. The article published in Physical Review E studies the decision-making processes across different cicada communities in a region, and the model they used has a lot of similarities to mathematical models developed for analyzing stock markets. Mathematics helps to study the behavior of different kinds of crowd decisions.
❁❁❁
What is going on in this graph?
What is the most pleasant language in the world? The Economist says Tok Pisin. Tok Pisin is a creole language spoken in Papua New Guinea
❁❁❁
Math Art: A Bird in Flight by Hamid Naderi Yeganeh
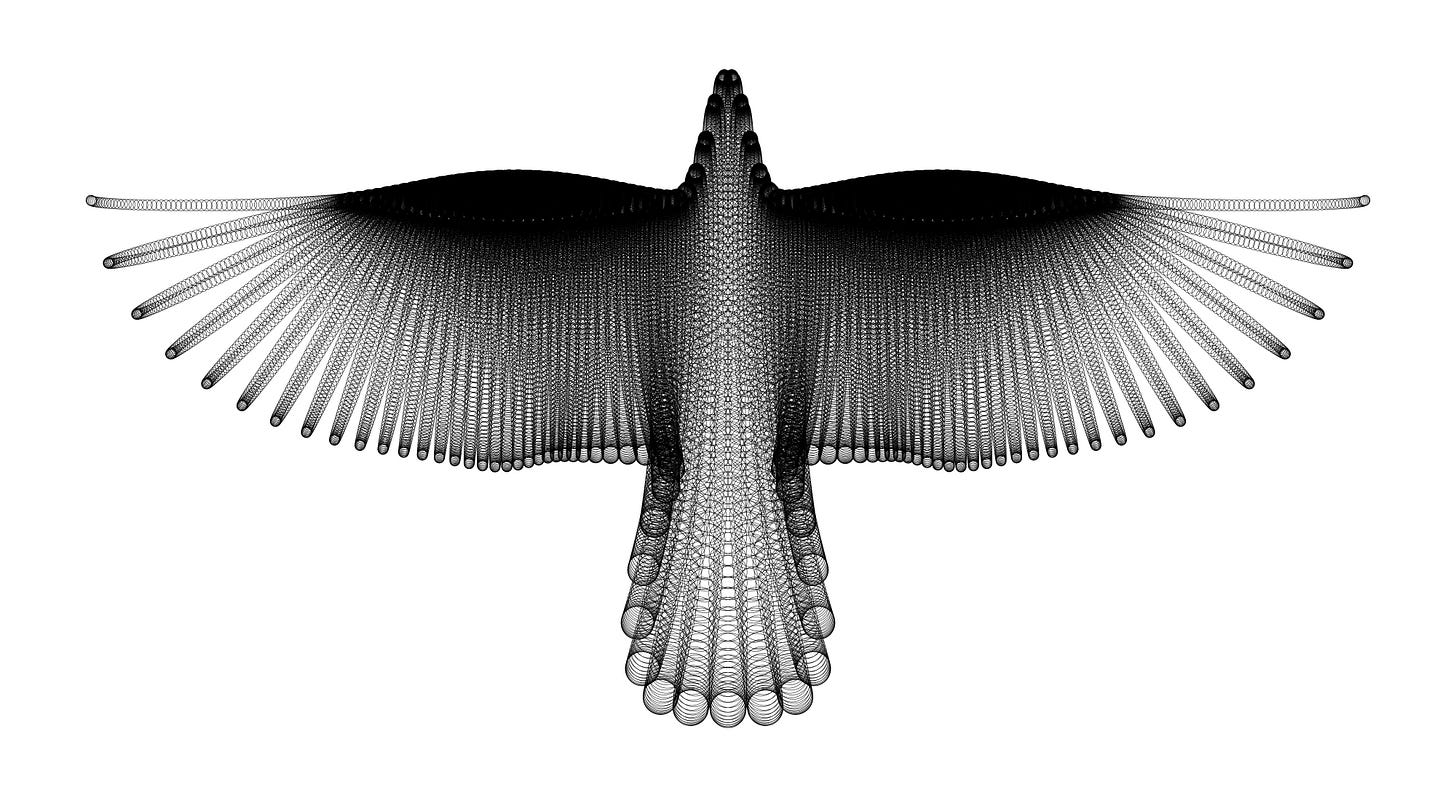
The artwork is made of 20,001 circles.
❁❁❁
Mathemania: Funny Math from the Internet
❁❁❁
I hope you enjoyed the Math Intercept. See you the next time!