The Math Intercept 9
STEAM WEEK, Bike Geometry, New Unique Proof to Pythagorean Theorem, The Problem of Calisson and more...
Greetings math world,
Since the last time, we have had STEAM Week in our school. Students participated in various events designed by their Science, Design, Math and Art teachers. I, myself organized a few board game sessions and the above competitions. The Lowest Unique Number challenge drew a lot of attention. This simple looking game has an interesting nature. When we played in class, students had a lot of fun. In the first rounds (we were playing with 17 students) the winning numbers were pretty small, like 2 or 4. Later rounds this changed to higher numbers like 8. In the school-wide case, the average of the numbers chosen by middle and high schoolers was 18. The winner (lowest unique number) was 25 however. Some numbers like 11 or 4 were chosen more than 6 people. Some were chosen by just two. (8 and 15) This year we told students that odd numbers, especially 7 and 13 were selected a lot in the past. This was a spoiler perhaps, but everyone was given the same information. This created a new confusion. Some considered this as a risk to take and chose 7 or 13. At the end 25 was chosen by 1 student. In the primary section, 8 was winner. 9 and 10 were also selected by one student only. Nobody chose 6. Only two students chose 4, while there are many 3s and 5s.
Bike Geometry Calculator is an online app where you can design your own bike by changing different dimensions and lengths below. With this app you can 1)Analyze an existing bike, 2)Fill in the gaps on a manufacturer's chart, 3) Compare two bikes, 4)Try before you buy, 5)See how component changes affect fit
Math Eyes:
Prayer in Mecca on the night of Ramadan 27
A nice drone view of Muslims praying during a Friday Prayer. Kaaba is the square at the center. (Photo credits: 3ajel_every_time on Instagram)
Math In Action
Viviana Di Pietro and colleagues discovers and explains that South American stingless bees follow mathematical traditions in building their nests.
Scientists recently discovered that a bacterium has an enzyme type that has a fractal structure. This is the first identification of fractal patterns on molecular level.
PBS has a series titled Doodles and Digits that is designed to make math relevant and understandable for upper elementary school children. The program aims to show the links mathematical concepts like fractions, geometry, and decimals to real-life scenarios, ignite a passion for math by demonstrating its practical applications in our daily world. Check this link for more. How It Is Math?
Two high school students from the US found a new original proof to the Pythagorean Theorem. This is an amazing achievement as the proof is done by two teenagers who were still high school students. Moreover they also disprove that trigonometric proofs of the Pythagorean theorem is not impossible as it was once thought to be. They came up with the proof in 2023, but I have learned about that after their achievement was showcased on PBS’ 60 Minutes recently. You can view their work here and watch a step-by-step explanation here.
Did you know that there is a mathematical order in chaos regarding the movements of the crowds? A research article published in Science magazine and coauthored by Karol A. Bacik, Bogan S. Bacik and Tim Rogers explains that crowds naturally organize themselves into walking lanes, even though no one tells them to do it. This is called "spontaneous lane formation." People just sort of fall in line with others moving the same way, creating two lanes roughly the width of two people each. If someone tries to walk the opposite way, they'll get gently nudged by the flow of people to switch lanes and go with the traffic. It's pretty amazing how this orderly system emerges all on its own! The researchers used differential equations and and made several experiments and found that the paths can take parabolic or elliptic shapes in different situations. Victoria Toro explains that this research can be helpful understanding crowd movements in tight spaces. It is key to keeping people safe during emergencies like Halloween stampede that happened in Korea in 2022 and the stampede happened during the pilgrimage in Mecca in 2015.
Proofs Without Words
The Problem of Calissons
Theorem: In any packaging, the number of calissons with a given orientation is one-third of the total number of calissons in the box.
Proof
Source: jstor
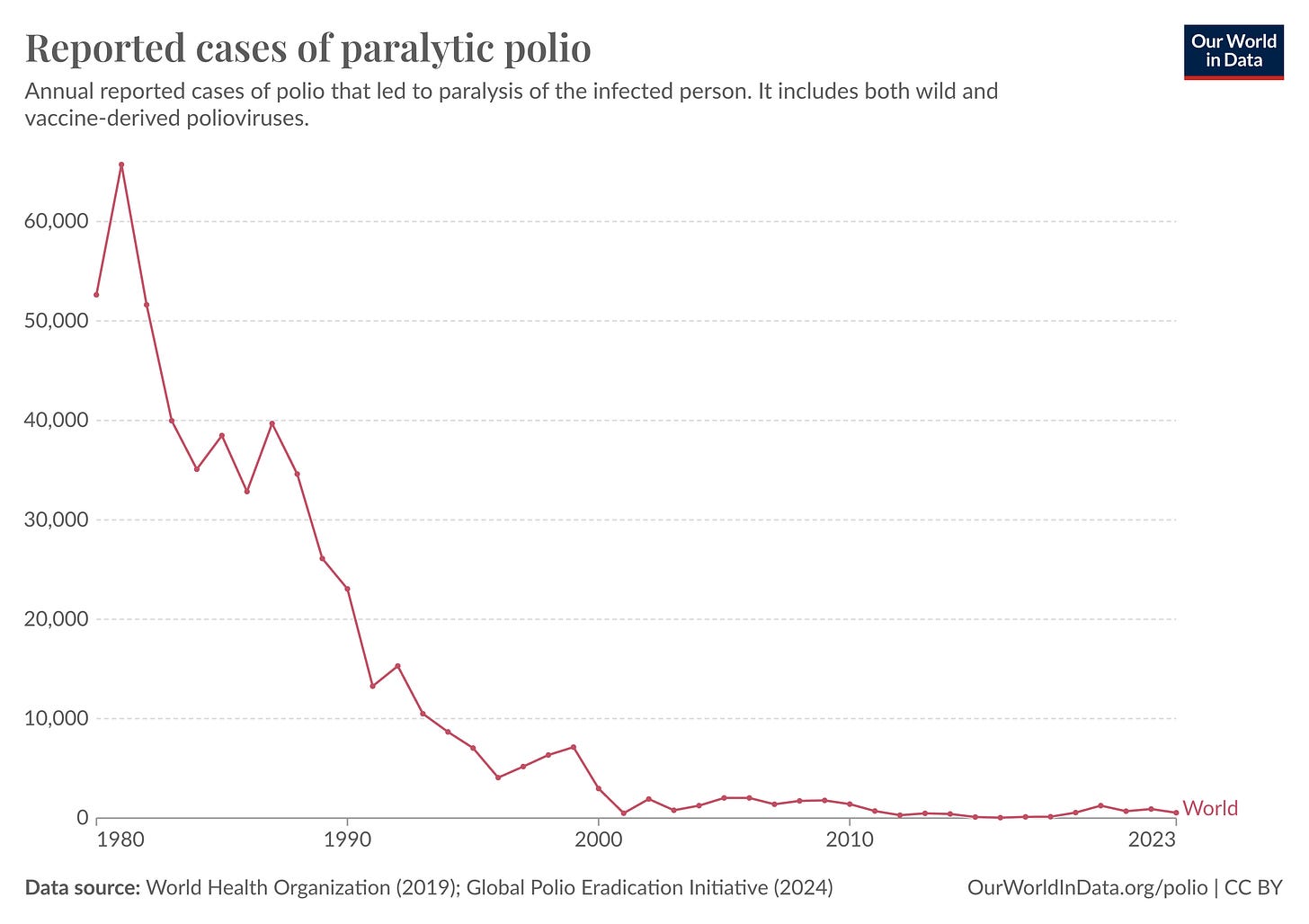
What is going on in this graph?
Polio is a highly contagious viral illness primarily affecting young children. It carries the potential for paralysis, permanent disability, and even death. During the early 1980s, documented annual cases exceeded 50 000, with a likely under-reporting that could have resulted in true figures exceeding 300 000 in peak years.
However, recent years have witnessed a dramatic decline in reported cases, with a recent update reflecting only 536 paralytic polio cases worldwide recorded in the past year. This significant reduction is largely attributed to global initiatives focused on improved vaccination coverage, alongside enhanced screening and testing protocols. After its establishment in 1988, the Global Polio Eradication Initiative (GPEI) played a pivotal role in coordinating these efforts.
Eradicating polio on a global scale remains a feasible objective, achievable through sustained high vaccination rates, meticulous case detection through comprehensive screening and testing, and the prompt implementation of high-quality immunization campaigns to effectively contain outbreaks.
This information and the graph is taken from Our World in Data. For details and regional statistics check here.
Curious Puzzles
Ask a friend to pick a number from 1 through 1000. After asking them 10 questions that can be answered with yes or no, you tell them the number. What kind of questions should you ask your friend so that you find their number? (Kordemsky, The Moscow Puzzles)
Can you find the values of the letter making the following equation correct?
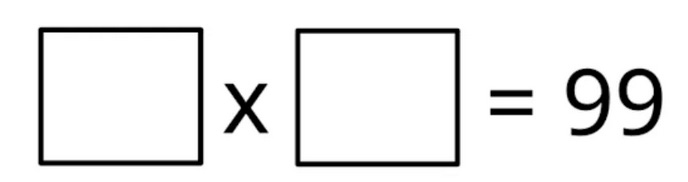
Find two rational numbers to fill the boxes. They must be both less than 10.
This puzzle is from Sam Blatherwick.
Solutions to Last Issue
3 is the highest number that cannot be achieved. Every even number can be found by repeated addition of two, and every odd number above 3 can be achieved by 2k+5.
11^149 (a bit silly answer, I will admit)
Moving two sticks to fix this equation: VII-V=II (many other solutions possible)
Chris Smith’s puzzle is a creative one.
Math In Art: Typus Arithmeticae by Gregor Reisch, [1503].
Mathemania